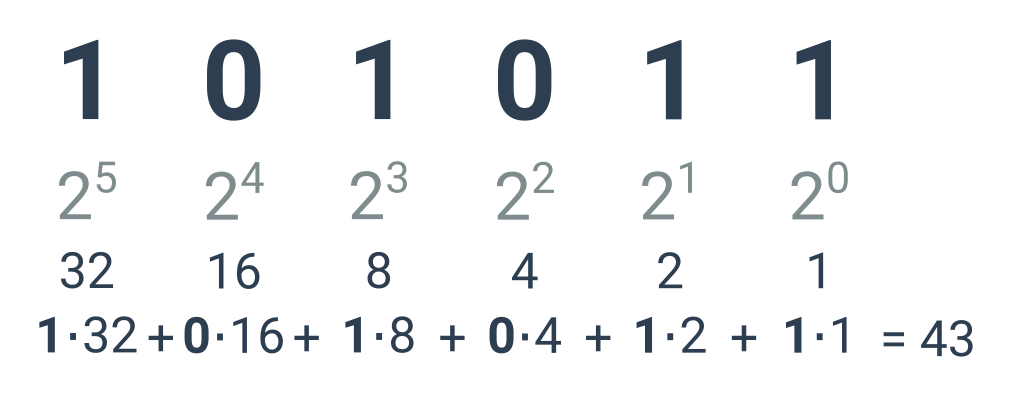Binárne čísla: základy

Princíp binárnej sústavy
V binárnej (dvojkovej) sústave zapisujeme čísla iba pomocou dvoch číslic: 0 a 1. Pozícia každej číslice v zápise zodpovedá určitej mocnine dvojky. Mocniny sa vždy začínajú nultou mocninou v prípade číslice najviac vpravo a zvyšujú sa smerom doľava. Hodnotu binárneho čísla potom vypočítame ako súčet týchto mocnín. Každú mocninu započítame, ak je na príslušnej pozícii 1 alebo nezapočítame, ak je na danom mieste 0.
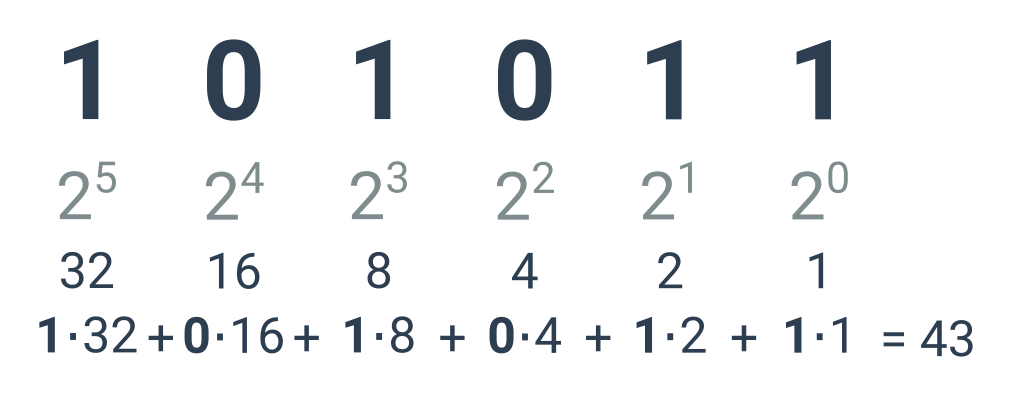
Značenie sústav
Aby sme odlíšili, či hovoríme o čísle v binárnej alebo v desiatkovej sústave, pridávame k číslam dolné indexy značiace sústavu. Napríklad číslo 5 v desiatkovej sústave budeme písať ako 5_{10}, binárne číslo s hodnotou 5 napíšeme ako 101_2. Potom môžeme jasne rozlíšiť, že napríklad zápisom 11_{10} myslíme desiatkové číslo 11, kým zápis 11_2 budeme interpretovať ako binárne číslo 11 a teda desiatkové číslo 3.
Intuitívna pomôcka
Pre základnú predstavu o binárnych číslach môžeme použiť pomôcku, ktorú máme vždy poruke – totiž ruku samotnú. Predstavme si, že si na prsty ruky napíšeme mocniny dvojky:
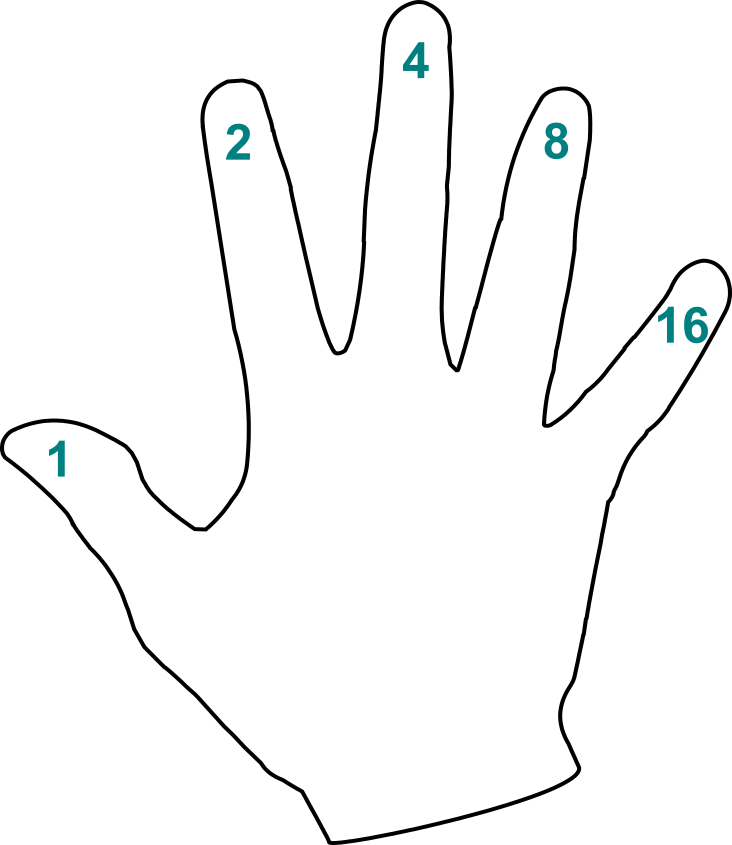
Potom môžeme na prstoch jednej ruky počítať nielen do päť, ale až do tridsaťjeden. Každé číslo je totiž možné vyjadriť (jednoznačne) ako súčet mocnín dvojky. Ak polohu prstov zaznačíme pomocou núl a jednotiek, dostaneme zápis v binárnej sústave.
Príklady čísel zapísaných v binárnej sústave
| 1 |
1 |
1 |
| 2 |
2 |
10 |
| 3 |
2+1 |
11 |
| 4 |
4 |
100 |
| 5 |
4+1 |
101 |
| 6 |
4+2 |
110 |
| 7 |
4+2+1 |
111 |
| 8 |
8 |
1000 |
| 9 |
8+1 |
1001 |
| 10 |
8+2 |
1010 |
| 16 |
16 |
10000 |
| 20 |
16+4 |
10100 |
| 30 |
16+8+4+2 |
11110 |
Zatvoriť